Graph Theory: Degree Sequence Algorithm ft Krita

Heyy! Welcome Back to my blog!

 Today we are doing Graph Theory. I somehow always get scared when someone mentions Graph theory. I have to overcome the fear. So here we go! I am writing some important theorems, terms, problems, etc that I learnt from the GT book. In short, Notes.

Book referred: Daniel A Marcus, Graph Theory, A Problem Oriented Approach

Chapter A:

• Graph: A graph consists of points, which are called vertices and connections, which are called edges and which are indicated by line segments or curves joining certain pairs of vertices.
• Degree: The degree of a vertex in a graph is the number of edges that occur at the vertex. The notation $d(a)$ represents the degree of vertex $A$.
• Degree Theorem: In any graph $G$, the sum of all the degrees is equal to twice the number of edges.
  
  This is because each edge contributes $2$ to the sum of degrees i.e when an edge is removed,  $\sum_{v\in G}d(v)$ decreases by $2.$
  
  
• Complete Graph: If all of the vertices in a graph are adjacent to each other, then the graph is called a complete graph. It is denoted as $K_n.$
• Path in a Graph: Repetition is allowed 
• Cycle: A cycle in a graph is a closed path in which the only repetation is the first and last vertex.
• Cycle Graph: A cycle graph containing $n$ vertices is denoted by $C_n.$
  
  
  
  
  
  
• Complement of a Graph: The complement of a graph $G_1$ is another graph $G_2$ having the same set of vertices but including only those edges that are not in $G_1.$

• Connected Graph: A graph is connected if every vertex is joined to every other vertex by a path. 
• Disconnected Graph: Not connected.
• Component: If a graph is disconnected, then it consists of two or more components. Each component is a connected subgraph $H$ whose vertices are not adjacent to any vertices not in $H.$
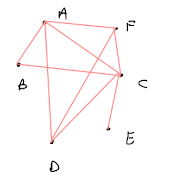
• Degree Sequence: The degree sequence of a graph is a list, or a sequence, of all the degrees of the vertices in the graph, including repetitions, usually in decreasing order.
   
  
  
  The above graph has degree sequence $(5,4,3,2,2,1).$
  
• Distance: The distance between two vertices in the same component of a graph is the length of the shortest path joining these vertices. 
• Diameter: If $G$ is a connected graph, then the diameter of $G$ is the maximum of all of the distances between vertices of $G.$
• Max and Min degree: The maximum degree in a graph is denoted by $\Delta$ and the minimum degree $\delta$.

The Degree Sequence Algorithm:

• Start with the terms of the sequences in decreasing order.
• Remove the largest term $m$ and reduce the next $m$ terms each by $1.$
• Rearrange the new sequence in decreasing order ( If needed)

The original sequence is the degree sequence of some graph iff the new sequence is.

Proof: Note that if the new sequence is graphic then clearly the old sequence is graphic too ( just add a new vertex.

Other direction. Let the degree sequence be $(s,d_1,d_2,\dots,d_s,t_1,\dots,t_n).$ And let $G$ be the graph for the degree sequence. Also, denote $v(i)$ as the vertex with with degree $i$. 

Now, we delete $v(s)$ from $G.$ 

If $v(s)$ is adjacent to $d_1,d_2,\dots,d_s$ then we are done.

So say, $v(s)$ is not adjacent to $d_j.$ Hence, it must be adjacent to some other vertex say $t_l.$ 

If $t_l=d_j$ then we can just swap them.

If $d_j>t_l$ then $v(d_j)$ is adjacent to some vertex $w$ that $v(t_l)$ isn't. 

Hence we can join $v(d_j),v(s)$ and $v(w),v(t_l)$ and remove the edge $v(d_j),v(w)$ and $v(s),v(t_l).$

And we can continue this process and make every $v(d_i)$ adjacent to $v(s).$

Problem 1: Prove that if $G_1$ and $G_2$ are complementary graphs, then at least one of them must be connected. 

Proof: Let's say $G_1$ is disconnected then let vertex $u,v$ be two vertices in same component and $w$ be in the other component. Clearly $uw,vw\not \in G_1\implies uw,vw\in G_2\implies$ there is a path between $u,v$ in $G_2.$ 

Hence in $G_2,$ the diameter is $2.$ 

Problem 2: Suppose that a graph contains $11$ vertices and that each vertex has a degree $5$ or greater. Prove that the graph must be connected.

Proof: Let's say for the sake of contradiction, the graph is disconnected. Then we consider the components. Note that there must be at least $2$ components and each component must have at least $6$ vertices since each vertex has a degree $5$ or greater. But this is not possible.

Problem 3: Show that in a graph with $n$ vertices, if $\delta +\Delta$ is greater than or equal to $n-1$ then the graph is connected.

Proof: If not, then consider the components. Clearly, there will be at least two components. So at least one component has $\Delta +1$ vertices and the other will have at least $\delta +1$ vertices. So the number of vertices would be at least $\Delta+\delta +2> n.$ Not possible.

Problem 4: Prove that in any graph with minimum degree $\delta ,$ there exists a simple path of length greater than or equal to $\delta .$

Proof: Let $\lambda$ be the length of the longest simple path. Then the endpoints of the longest path will have degree $\le \lambda.$ But the endpoint will have at least $\delta.$ So $\delta\le \lambda.$

Chapter B:

• Isomorphism is graphs: If two graphs are isomorphic then they have the same number of vertices, the same number of edges, the same maximum and minimum degrees, same degree sequence, same length of the longest simple path, same cycle lenghts.
  However, satisfying this doesn't imply two graphs are isomorphic.

Chapter C:

• Bipartite Graphs: It is a graph whose vertices can be separated into two sets $X$ and $Y$ in such a way that every edge in the graph has one endpoint in each set.
  
  Here we have $X=\{A,C,F\},Y=\{B,D,E\}$
  
  
  
  
  
  
• Complete Bipartite Graphs: Every vertex in $X$ is adjacent to every vertex in $Y.$ They are denoted by symbol $K_{m,n},$ where $m$ and $n$ are vertices in $X$ and $Y.$
  
  Note that $K_{m,n}$ will have $mn$ edges and vertices in $X$ set will have degree $n$ and vertices in $Y$ set will have degree $m.$
  
  Here is $K_{2,5}.$
  
  
  
  

  Cycle Theorem for Bipartite Graphs: A graph is bipartite iff it contains no odd cycle.
  
  Proof: If the graph contains an odd cycle then it's not bipartite (colour the vertices, we won't be able to divide into two sets cause it's odd). 
  If the graph contains no odd cycle, then choose any vertex $A$ from any component of Graph $G.$ Assign it colour red and then colour the vertices adjacent to it Blue and then vertices adjacent to Blue vertices as Red and so on along simple paths from $A.$
  
  Note that no vertex will have two distinct colours. 
  Proof: Suppose not. Let the vertex be $W.$ Then we get $A\rightarrow W\rightarrow A$ an odd cycle.
  
  

Chapter D:

• Tree: It is a graph that is connected and contains no cycles.
  
• Forest: It is a graph in which each component is a tree.
• Spanning Tree: A tree which is a subgraph of graph $G$ and contains every vertex of $G.$ Any connected graph would have a spanning tree.
  
  
  
  
  

Pruning a Tree: Removing a vertex of degree $1$ from the tree along with the edge that occurs at that vertex. 

Here is the example,

Note that after pruning, we still get a tree.

Lemma: Prove that every tree with two or more vertex has at least two leaf vertices.
Proof: Consider the longest simple path in the tree. Let the end points be $A,B.$ Let the other vertices of the graph not in the path be $d_1,d_2,\dots,d_n$ and vertices in the path be $v_1,\dots,v_k.$ Let $v_i,v_j$ be adjacent to $A,B$ respectively.

Note that $d_1,d_2,\dots,d_n$  are not adjacent to $A,B$ since we considered the longest path and $A$ is not adjacent to $v_1,\dots ,v_{i-1}v_{i+1},\dots,v_k$ else it would form a cycle. Similar to $B.$ Hence $A,B$ have degree $1.$

Tree Theorem 1: Every tree with $v$ vertices has exactly $v-1$ edges.
Proof: Just prune it. $v-e$ is always $1.$

Forest Corollary: In a forest with $v$ vertices and $k$ components, the number of edges is $v-k.$
Proof: Each component has $v-e=1.$ 

Tree Theorem 2: In any Tree, there is exactly one simple path from any vertex to any other vertex.
Proof: Since $T$ is connected, there is a simple path. If there are two different paths then we will get a cycle.


Cayley's Formula: In a labelled complete graph with $n$ vertices, the number of spanning trees is $n^{n-2}.$

We prove it using Prufer's method which establishes a bijection between spanning trees and sequence of $n-2$ length which can be filled up in $n^{n-2}$ ways since we have $n$ numbers.

Converting the spanning-tree into Prufer's sequence: 
First label the graph with numbers. Now we construct the sequence $S.$

• Find a leaf with the smallest label
  
• Include the neighbour of the leaf and then delete the leaf 
  
  

Problem 1: Show that the average degree a tree in a tree is always less than 2. 
Proof: The number of edges is $n-1$ and the number of vertices is $n.$ So the sum of degrees is $2n-2<2n.$

Problem 2: Show that the number of vertices of degree $1$ in any tree must be greater than or equal to the maximum degree $(\Delta)$ in the tree.
Proof: Let $A$ have degree $\Delta .$ Consider the $\Delta$ subgraphs formed by $A.$ Each will be a tree and will be disconnected ( or else we get cycle). Each tree will have one leaf. So we get $\Delta$ leaves.

Problem 3: Show that if a graph has $v$ vertices and $v-1$ edges and contains no cycle. It's connected.
Proof: If not, let there be $k$ components. These components are connected and have no cycles, hence a tree. Then we will have $v-k$ edges.

Problem 4: Show that if a graph has $v$ vertices and $v-1$ edges and is connected, then the graph has no cycles.
Proof: Since it is connected, the graph contains a spanning tree. The spanning-tree contains $v-1$ edges. Hence the graph is a tree.

Three conditions:

If graph $G$ satisfies any two of three conditions;
1. $G$ has $v$ and $v-1$ edges
2. $G$ is connected
3. $G$ contains no cycles,
then $G$ satisfies all three conditions.

Yep, this was it for the Part A of the book! I also made my first Digital Art on Krita! It did take me a lot of time. How is it?

Yee, that's it for today's blog. I will post the sequel tomorrow.

Sunaina 💜